高調波所論 [REPORT5-1] フーリエ級数による整流回路の検証
| (1)このリポートのテーマ |
| (2)整流回路の諸特性 |
| (3)分析ツール |
| (4)整流回路の交流側電流波形の検証 |
| (5)整流回路の直流側出力波形の検証 |
| (6)整流回路の直流側出力波形のL分による平滑の検証 |
| (7)方形波インバータのL分を含む負荷側電流の検証 |
| (8)まとめにかえて |
高調波所論 [REPORT5-1] フーリエ級数による整流回路の検証
| (1)このリポートのテーマ |
| (2)整流回路の諸特性 |
| (3)分析ツール |
| (4)整流回路の交流側電流波形の検証 |
| (5)整流回路の直流側出力波形の検証 |
| (6)整流回路の直流側出力波形のL分による平滑の検証 |
| (7)方形波インバータのL分を含む負荷側電流の検証 |
| (8)まとめにかえて |
| ・変換回路は無制御状態(α=0)とする。 |
| ・転流は無視する。 |
| ・交流電圧は対称正弦波とする。 |
- 高調波分析プログラムで検証したい項目とその値を次表にまとめてみた。リアクトルによる完全平滑の場合で、交流側電流波形は矩形波として扱う。
整流回路 単相半波 単相全波 三相半波 三相全波 パルス数 1 2 3 6 12 24 最大直流電圧 0.450 0.900 1.17 2.34 2.34 交流線路力率 0.637 0.900 0.826 0.955 0.989 0.997 直流 交流 直流 交流 直流 交流 直流 交流 直流 交流 直流 交流 調波次数 1 111 100 100 100 100 100 100 2 47.1 47.1 50 3 33.3 33.3 17.7 4 9.4 9.4 25 5 20.0 20.0 20 20 6 4.04 4.04 4.04 4.04 7 14.3 14.3 14.3 14.3 8 2.25 2.25 12.5 9 11.1 11.1 1.77 10 1.43 1.43 10 11 9.1 9.1 9.1 9.1 9.1 12 0.99 0.99 0.99 0.99 0.99 13 7.7 7.7 7.7 7.7 7.7 14 0.73 0.73 7.1 15 6.7 6.7 0.63 16 0.55 0.55 6.2 17 5.9 5.9 5.9 5.9 18 0.44 0.44 0.44 0.44 19 5.3 5.3 5.3 5.3 20 0.35 0.35 5.0 21 4.8 4.8 0.32 22 0.29 0.29 4.5 23 4.3 4.3 4.3 4.3 4.3 4.3 24 0.25 0.25 0.25 0.25 0.25 25 4.0 4.0 4.0 4.0 4.0 4.0 - 「直流」は、無負荷時の直流側電圧を100%とした時の各次高調波の実効値の割合である。また「交流」は、交流側電流の基本波成分を100%とした時の各次高調波の 実効値の割合である。
- 高調波含有率の表から重要な二つの結論が導かれる。
- 変換回路のパルス数が、発生する高調波成分の次数を決定する。
- 発生する高調波成分の大きさ(振幅)は次数のみに依存し、変換回路のパルス数には無関係である。
- 整流回路で直流側をリアクトルで平滑すると、交流側電流波形は方形波となる。またコンデンサ平滑では「鬼の角」波形や「うさぎの耳」波形となる。 ここでは各種整流回路におけるいわゆる高調波力率がどのような値になるか、分析ツールを駆使して検証する。また交流側電流波形に含まれる高調波含有率についても検証する。 分析結果の高調波含有率については、ここでは基本波を100%としたグラフを参照していただきたい。
- 高調波力率μは次のように定義される。ただし交流側電源電圧は対称正弦波形とする。
μ=I1/I
I1:基本波実効値
I:波形の実効値- 「鬼の角」波形
データ ① を「入力例」シートからコピーする。単相全波整流をコンデンサで平滑した時の交流側電流波形である。 「鬼の角」波形では、μ=0.585 程度となっている。パソコンや多くの家電製品がこの程度の力率になっているらしいので、概ね正しいと思われる。
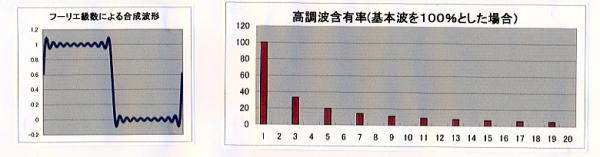
- 「うさぎの耳」波形
データ ② を「入力例」シートからコピーする。三相全波整流をコンデンサで平滑した時の交流側電流波形である。 μ=0.744 程度となっている。ただし入力データは回路が三相と考え私が適当にデータ化したものなので、信頼性はない。 正しいデータをお持ちの方は教えていただきたい。
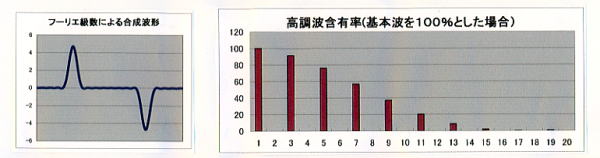
- 「矩形波 単相半波整流」波形
データ ④-2 を「入力例」シートからコピーする。単相半波整流をリアクトルで平滑した時の交流側電流波形である。 理論値はμ=0.637 である。分析値はμ=0.640 程度になっている。ただし、この値は波形実効値として直流分を含んだ場合である。 交流分のみの実効値を対象にすると、全波整流の場合とほぼ同じのμ=0.909 程度となる。この違いの意味は、ただいま考え中である。
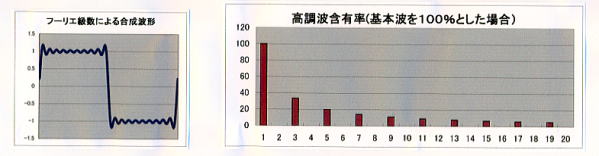
- 「矩形波 単相全波整流」波形
データ ⑤-2 を「入力例」シートからコピーする。単相全波整流をリアクトルで平滑した時の交流側電流波形である。 理論値はμ=0.900 である。分析値はμ=0.909 程度になっている。この差は分析が第20調波までを対象にしていることによるもので、 誤差の範囲内と考える。
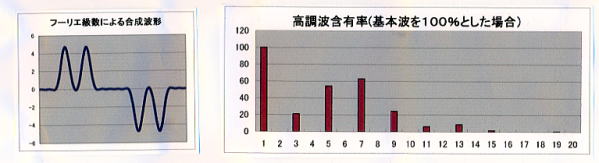
- 「矩形波 三相半波整流」波形
データを ⑥-2 を「入力例」シートからコピーする。三相半波整流をリアクトルで平滑した時の交流側電流波形である。 理論値はμ=0.826 である。分析値はμ=0.833 程度になっている。この差の原因も上記と同じである。ただし、この値は交流分のみを対象 とした実効値に対しての値であり、↑の単相半波の場合と反対になっている。この辺の考え方がよくわからない。
- 「矩形波 三相全波整流」波形
データ ⑦-2 を「入力例」シートからコピーする。三相全波整流をリアクトルで平滑した時の交流側電流波形である。 理論値はμ=0.955 である。分析値はμ=0.961 程度になっている。この差の原因も上記と同じである。
- ここでは負荷回路が抵抗分のみの場合に、各種整流回路の出力波形の高調波含有率がどのような値になるか、分析ツールを駆使して検証する。したがって 入力欄の下の回路成分入力欄は初期値のまま即ちR=1、L=0、C=0とする。分析結果のグラフは直流分を100%とした方を参照していただきたい。
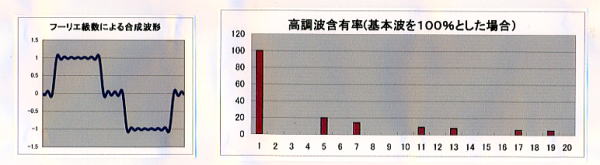
- 「単相半波整流」波形
データ ④-1 を「入力例」シートからコピーする。第2調波以下は次項の単相全波整流の値と全く同じであるが、基本調波分が 現われている。
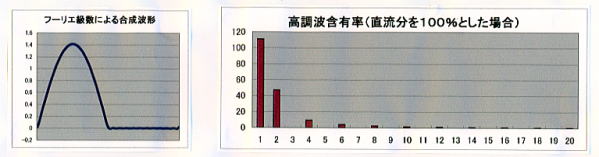
- 「単相全波整流」波形
データ ⑤-1 を「入力例」シートからコピーする。
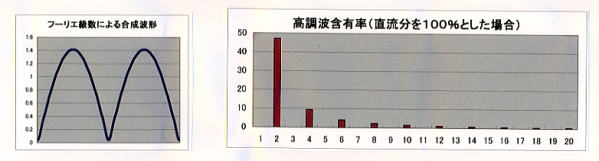
- 「三相半波整流」波形
データ ⑥-1 を「入力例」シートからコピーする。
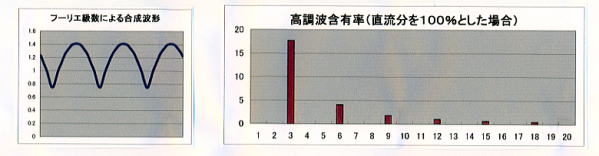
- 「三相全波整流」波形
データ ⑦-1 を「入力例」シートからコピーする。
- ここでは負荷がインダクタンス分即ち平滑リアクトルを含む場合に、各種整流回路の出力波形がどの程度平滑されるのか、分析ツールを駆使して検証する。 シート「係数分析」の入力表の下に回路成分入力欄があるので、L分を単位[H]で適当に入力して平滑度を検証していただきたい。なおC分の入力もできるが、平滑度の検証では C=0とする。またR分も変更できるが、ここではR=1のままとする。
- 「単相半波整流」波形
データ ④-1 を「入力例」シートからコピーする。このような入力電圧波形となるのは還流ダイオードを備えている場合である。 還流ダイオードを備えていない時は転流現象がないので、インダクタンスに蓄えられたエネルギーが電源側に返還されるため、整流ダイオードのオンの期間が延び、入力例のような 電圧波形とならない。
L=0.005[H]程度で還流ダイオードの影響がよくわかる。L=0.1[H]程度でかなり平滑されているのがわかる。
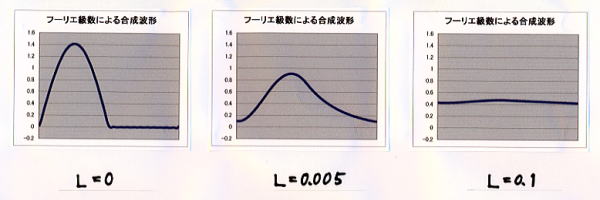
- 「単相全波整流」波形
データ ⑤-1 を「入力例」シートからコピーする。L=0.01[H]程度でかなり平滑され、L=0.1[H]程度で ほぼ平滑されているのがわかる。
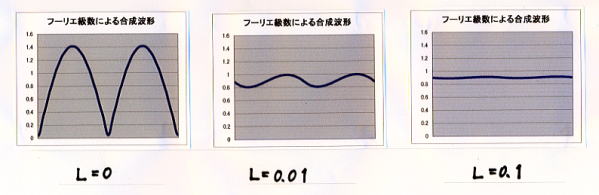
- 「三相半波整流」波形
データ ⑥-1 を「入力例」シートからコピーする。L=0.005[H]程度でかなり平滑され、L=0.05[H]程度で ほぼ平滑されているのがわかる。
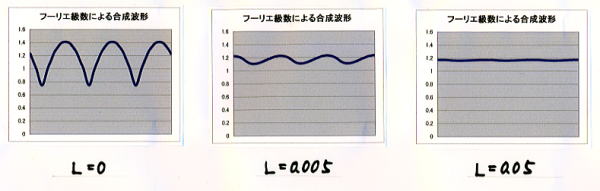
- 「三相全波整流」波形
データ ⑦-1 を「入力例」シートからコピーする。L=0.001[H]程度でかなり平滑され、L=0.005[H]程度で ほぼ平滑されているのがわかる。
- 方形波インバータの出力電圧波形は矩形波である。ここでは負荷にインダクタンス分を含む場合に電流波形がどの程度歪むのか、分析ツールを駆使して 検証する。入力方法は上記と同じである。負荷として力率0.8程度の電動機の場合、R=1[Ω]に対してL=0.002[H]程度である。
- 「単相全波整流」波形
データ ⑤-2 を「入力例」シートからコピーする。L=0.001[H]程度でかなり歪み、L=0.003[H]程度で ほぼ三角波になることがわかる。
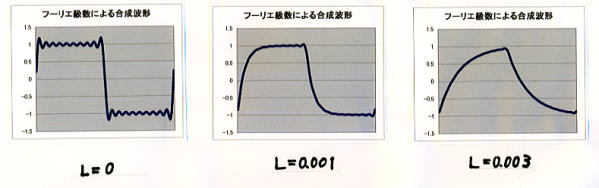
- 「三相全波整流」波形
データ ⑦-2 を「入力例」シートからコピーする。L=0.001[H]程度でかなり歪み、L=0.002[H]程度で 三角波に近くなるが、正弦波にも近くなっている。
- 単相半波整流および三相半波整流における交流側電流波形の高調波力率の計算方法が疑問のまま残ってしまった。解説書の理論値と同じ値が出るのであるが、 単相の場合は直流分を含んだ計算で、三相の場合は直流分を含まない計算値が理論値と等しくなってしまう。
- 単相半波整流の直流側出力波形に基本波分が111%現われるが、この意味がわからない。単相半波整流は最も単純に見えるが、その分析結果の意味は奥が深そうである。
- コンデンサ平滑も基本回路で分析できると考えていたが、これは単純ではないようである。もうしばらく勉強してからアップしたい。