ＫＩＭの電気リポート1

地絡について   ［ＲＥＰＯＲＴ１－６］  直接接地系における零相電圧の理論

（１）このリポートのテーマ
（２）直接接地系の具体例
（３）「零相電圧が相電圧の１／３」の誤解の原因

ＫＩＭの電気リポート１［目次］に戻る
ＴＯＰに［戻る］
サイドフレームを［消去する］


（１）このリポートのテーマ

零相電圧の定義として、Ｖ０＝－（Ｖａ＋Ｖｂ＋Ｖｃ）／３ がある。直接接地系で１線地絡として、 Ｖａ＝０ と考え、Ｖ０＝－（Ｖｂ＋Ｖｃ）／３ とベクトル的に考え、零相電圧が相電圧の １／３であるとする荒っぽい解釈がある。実は私もそう思っていた。図で表すとわかりやすい。



しかしそれはより正確に表現すると、多くの条件付で正しい、ということになる。このリポートではまず典型的な直接接地系の具体例を示し、結果的に零相電圧は相電圧の １／３程度になることを示す。次に有効接地について記し、最後に上記思い込みとなった原因を探る。このリポートの随所に対称座標法が出てくるが、直接接地系の議論では不可避な 手段であることを最初にお断りしておく。


（２）直接接地系の具体例
  1. 中性点を直接接地した２７５ｋＶ、３２０ｋｍの送電線で、発電所側（Ａ）から８０ｋｍの地点で故障が発生した場合の各リアクタンス値の概数は次のようになる。 ここで負荷側（Ｂ）は同期電動機としている。これらの値は、前川幸一郎著「対称座標法講義」の演習問題から引用したものである。

                発電機の正相過渡リアクタンス Ｘｇ１＝６５Ω
                同期電動機の正相過渡リアクタンス Ｘｍ１＝１４０Ω
                変圧器のリアクタンス ＸｔＡ＝ＸｔＢ＝２２Ω
                線路の正相リアクタンス ＸＡ＝２８Ω            ＸＢ＝８４Ω
                線路の零相リアクタンス Ｘ０Ａ＝９６Ω            Ｘ０Ｂ＝２９０Ω

    系統図と零相回路、正相および逆相回路を示しておく。



  2. これらの値から各対称分リアクタンスを計算すると、零相リアクタンスは８５．６Ω、正相リアクタンスおよび逆相リアクタンスは７８．４Ωとなる。 すなわち、この例の場合においては各対称分リアクタンスは結果的に同じような値となる。送電線の１線地絡時の零相電圧は次式で表される。

                 V0 = - Z0 Ea
    Z0 + Z1 + Z2

    そのため、この例の場合は零相電圧は結果的に相電圧のほぼ１／３となる。

  3. １線地絡時の健全相の電圧は次式で表される。

                 Vb = ( a² - 1 ) Z0 + ( a² - a )  Z2 Ea              Vc = ( a - 1 ) Z0 + ( a - a² )  Z2 Ea
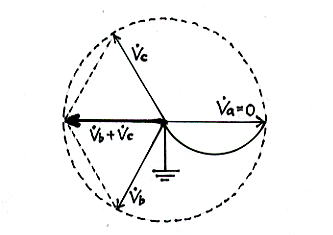
    Z0 + Z1 + Z2 Z0 + Z1 + Z2

  4. ここで、Ｚ０＝Ｚ１＝Ｚ２が成立すると、Ｖｂ＝ａ²ＥａおよびＶｃ＝ａＥａ となり、「このリポートのテーマ」で示した「零相電圧は相電圧の１／３」が導かれる。その条件は次の３点である。

    ①線路インピーダンスが無視できる。これが無視できないと、零相回路でのインピーダンスが正相回路でのインピーダンスの３．５倍となり、ややこしいことになる。
    ②発電機や負荷のインピーダンスが無視できる。
    ③変圧器のインピーダンスも無視してしまうと無限大の故障電流となってしまうので、変圧器インピーダンスは無視しない。

    しつこいようであるが大事なことなので、もう一度繰り返しておく。これらの条件下で、直接接地系の１線地絡時の零相電圧は相電圧の１／３となる、という論議が正しい。 しかし上記の例にもあるように、一番小さい変圧器のインピーダンスだけを残す、という非現実的な仮定であることも事実である。

  5. 送電系統における過渡状態での計算では、Ｚ１、Ｚ２はリアクタンス分のみと考えられ、実用上Ｚ１とＺ２は近似的に 等しい、としてよい。また直接接地系では中性点接地抵抗は無視できるので、 Ｚ０もリアクタンス分だけと考えて差し支えない。具体的には線路のインダクタンスと変圧器のリアクタンスである。架空送電線では対地静電容量による インピーダンスは大きい値となり、Π型回路を仮定して変圧器と並列になっているとしても、十分無視できる。

  6. 一般に、Ｚ０＝Ｒ＋Ｘ０とおき、０≦（Ｒ／Ｘ１）≦１かつ０≦（Ｘ０／Ｘ１）≦３の範囲では 健全相の対地電圧は相電圧の１．３倍を越えることはない。このような系統を「有効接地系」という。

  7. Ｒを無視し、Ｘ０／Ｘ１＝３のときの計算は次のようになる。

    Vb = ( - 0.9 - j 0.866 ) Ea
    Vc = ( - 0.9 + j 0.866 ) Ea
    Vo = - 0.6 Ea

    これをベクトル図で表しておく。



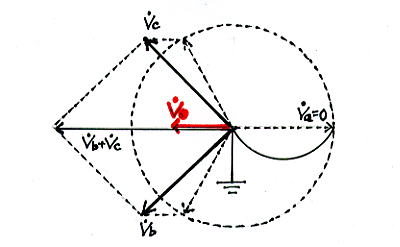
    この例では零相電圧はＥａのほぼ２／３となっている。このことからも「直接接地系では１線地絡時の零相電圧が相電圧 の１／３になる」という図式の誤りが理解できる。

（３）「零相電圧が相電圧の１／３」の誤解の原因
  1. 高抵抗接地系統や非接地系統では、零相インピーダンスに比べて正相インピーダンスや逆相インピーダンスは十分無視できる。その暗黙の（まさに知らず知らずの） 仮定を直接接地系にも当てはめているのである。無視できないものを、思い込みによって無視しているのである。

  2. もう一つが、「このリポートのテーマ」で示したベクトル図である。全く非の打ちどころのないよく見慣れた図である。しかしこれも同じ仮定の下でしか正しくないのである。 直接接地系ではこうはならないのである。

  3. 「直接接地系では１線地絡時の零相電圧が相電圧の１／３になる」と言うときは、以上の認識を持った上で言う必要がある。正確に言うなら 「直接接地系では１線地絡時の零相電圧が相電圧のほぼ１／３になる。」というべきである。

  4. 結論を言うと、直接接地系では各対称分インピーダンスを丁寧に計算して、零相電圧を求めなければならない、ということになる。
皆さんのご感想、ご意見をお待ちしています。


特報！！

超高圧送電系統の実務にも詳しいＹ．Ｔ氏からこのリポートについての感想をいただきました。掲載を承諾していただきましたので、是非ご覧下さい。
[直接接地系の保護]はＰＤＦファイルです。２５ｋＢで圧縮はしていません。


ＫＩＭの電気リポート１［目次］に戻る
ＴＯＰに［戻る］
ご意見、ご感想、ご質問は ［掲示板］ または［メール］でお願いします。